服务热线
023-63012636
服务热线
023-63012636
真正的艺术与美，
从来不是艺术馆里束之高阁的藏品，
而是自然界中的生灵与万物。
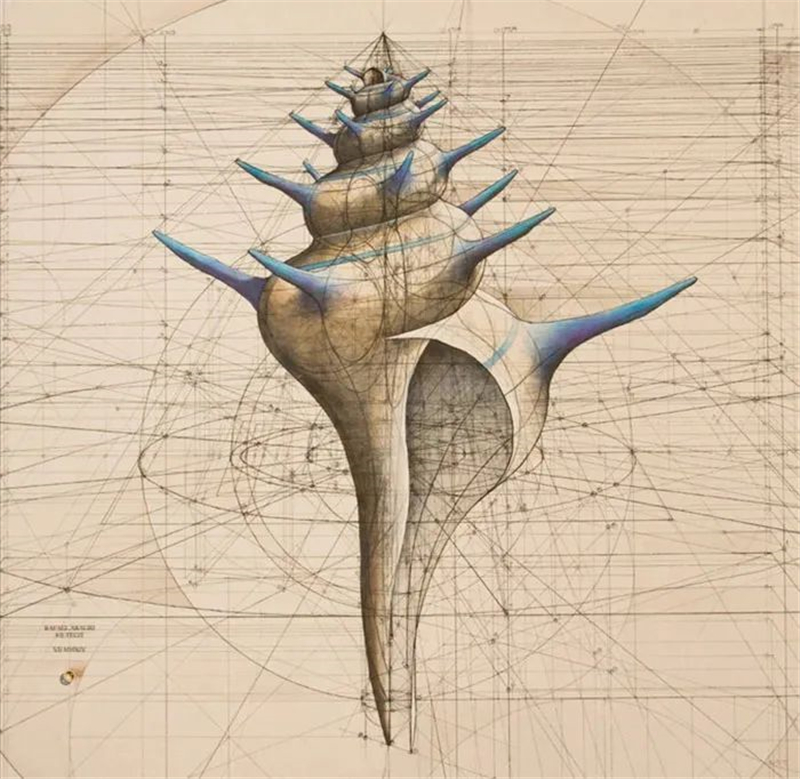
以上的三张全部都是
没有使用任何计算机绘图软件，
而是单靠铅笔、尺、量角器、
圆规等纯手绘出来的。
你能看出来吗？
对应的分别是海螺和蝴蝶的序列。
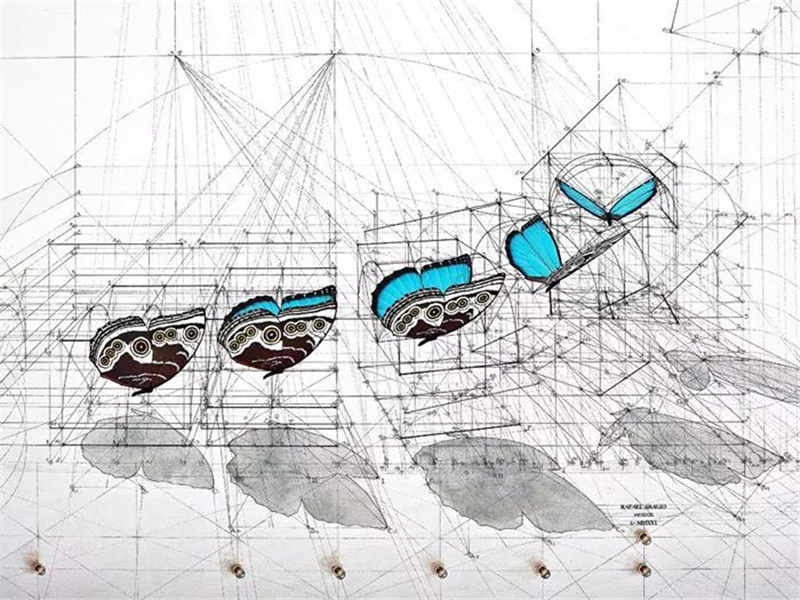
不同的数学序列经过不同的组合，
最后诞生出了不同的图案。
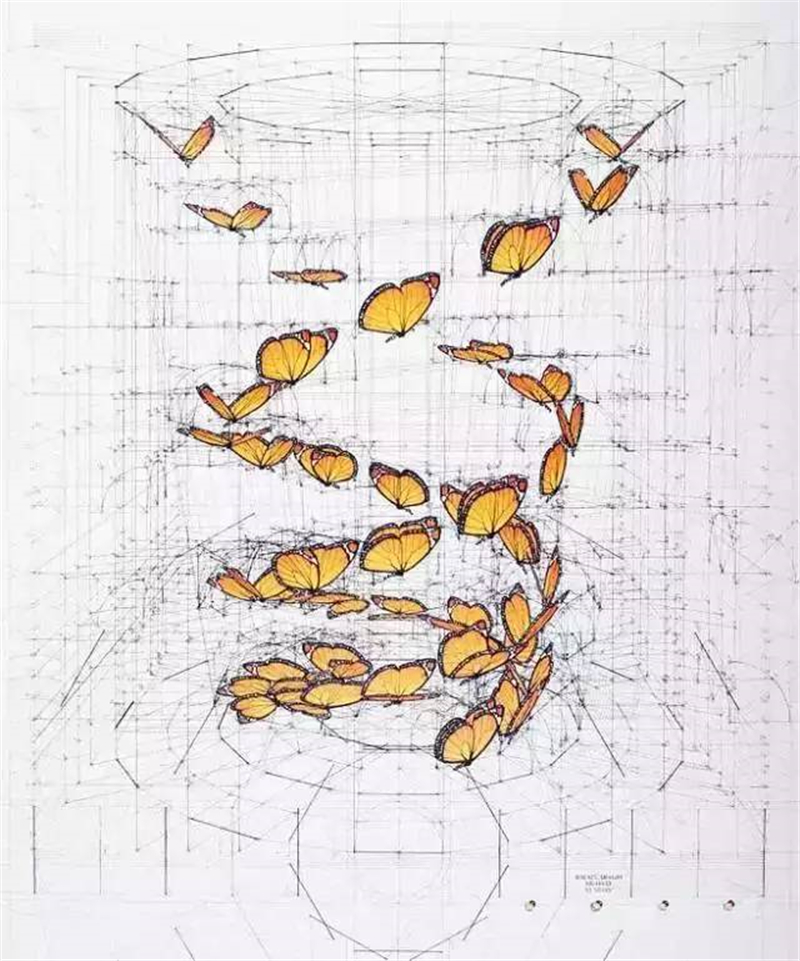
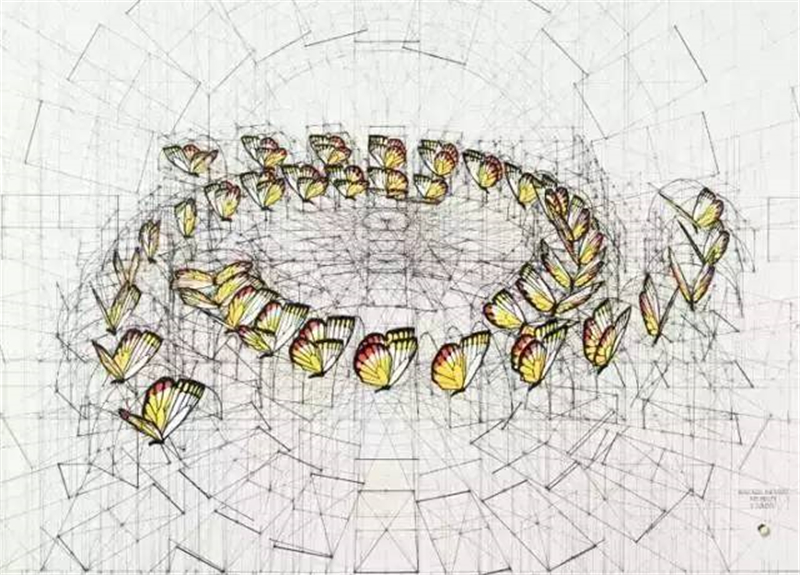
这些序列主要是由
著名的黄金分割、
黄金螺旋法则与斐波纳契数列，
与一些普通的对数曲线、
算术曲线和指数曲线
以及几何图案组成的。
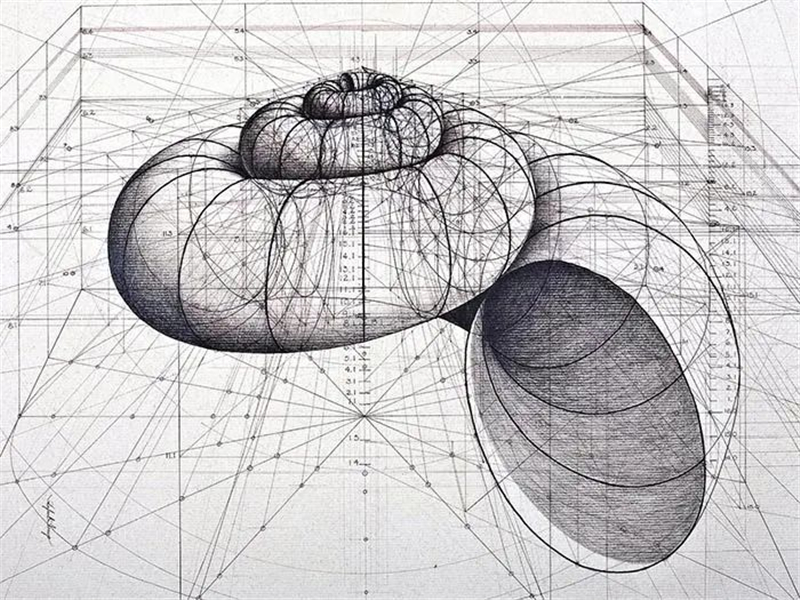
这个序列并不是人为创造的，
而是大自然创造后被人类发现的。
鲜花、飞鸟、动物、人体等等，
大自然中美的一切，
都和黄金比例有着极大的关系。
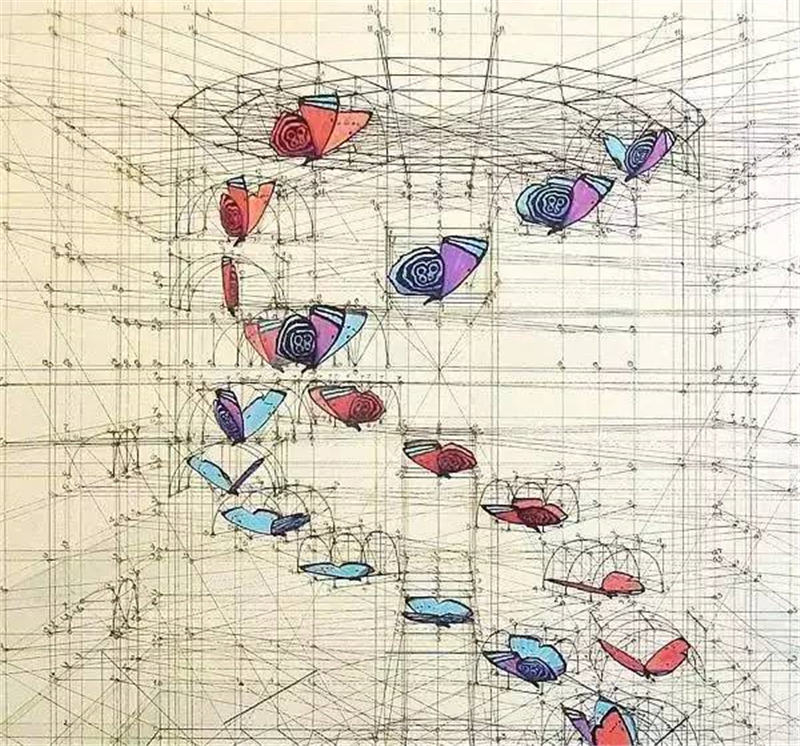
黄金比例，
有时候也叫作蝴蝶比例，
意思就是蝴蝶身长与双翅展开的长接近黄金分割比。
另外蝴蝶也符合蝴蝶曲线的理论，
这一切都让蝴蝶的外形看起来非常完美。
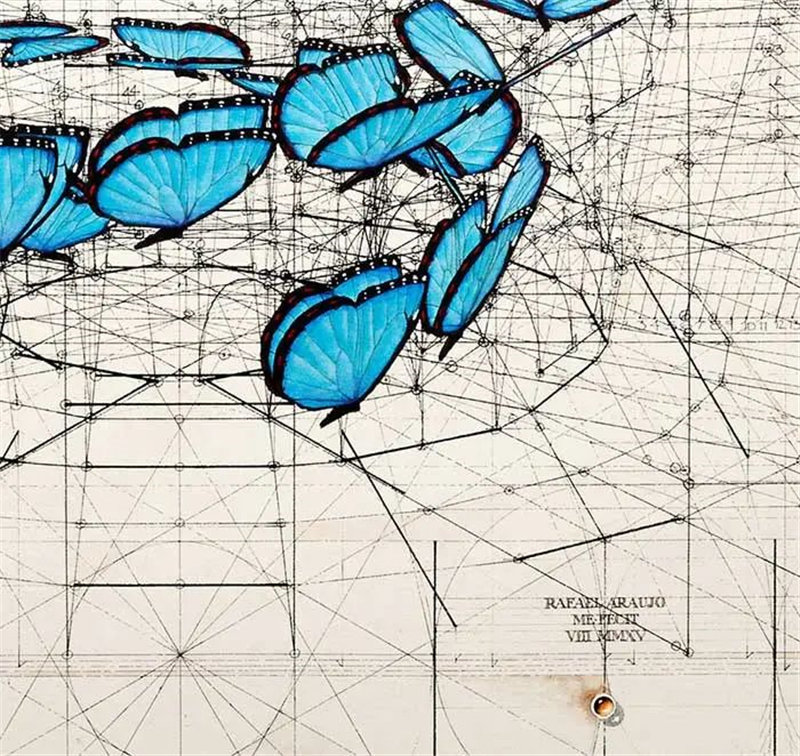
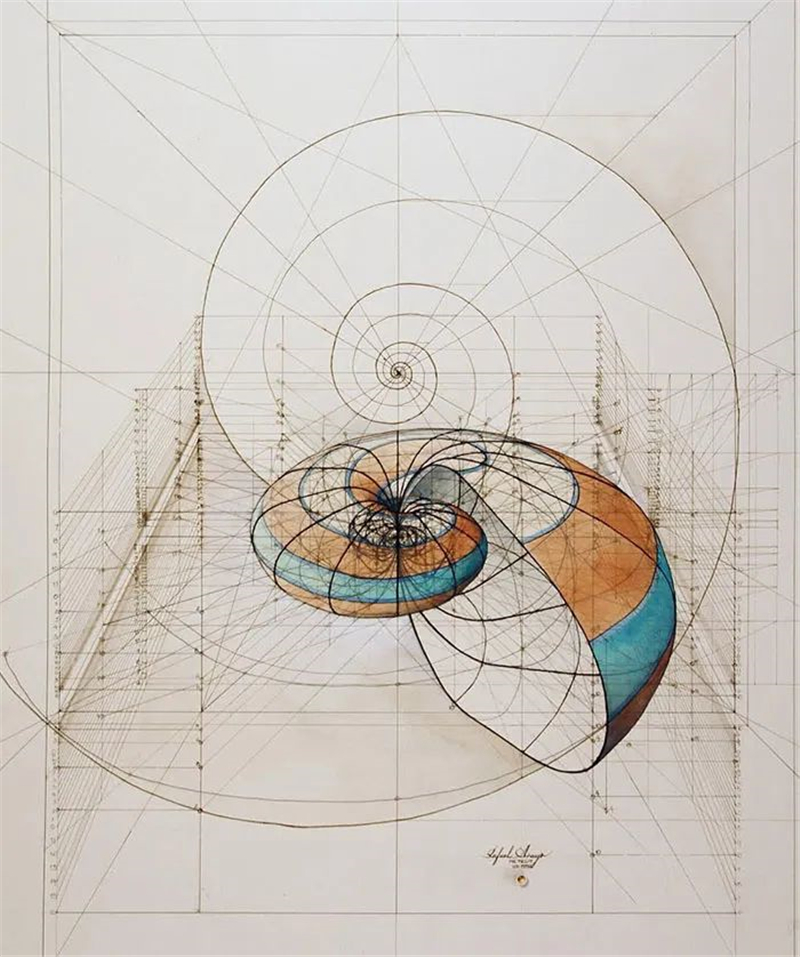
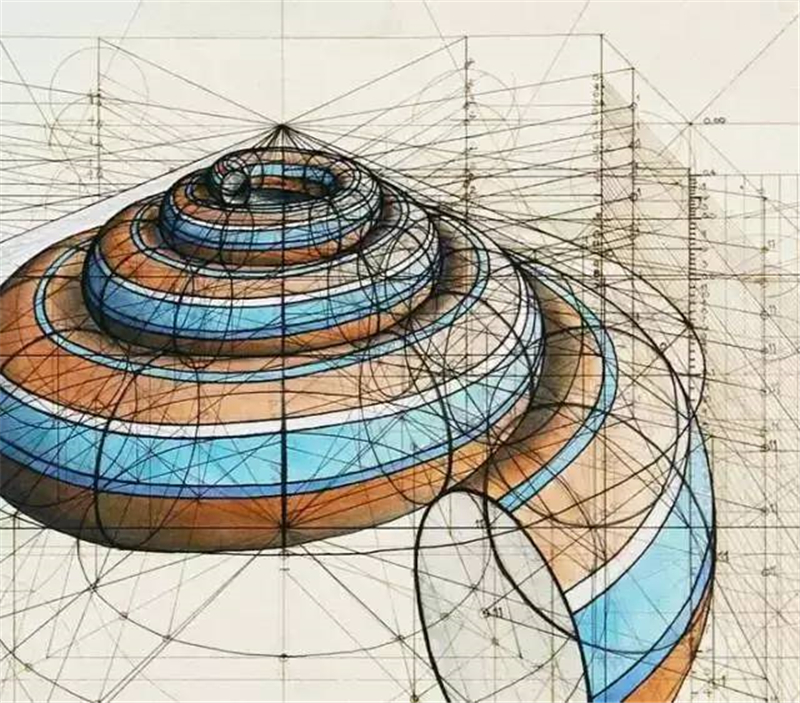
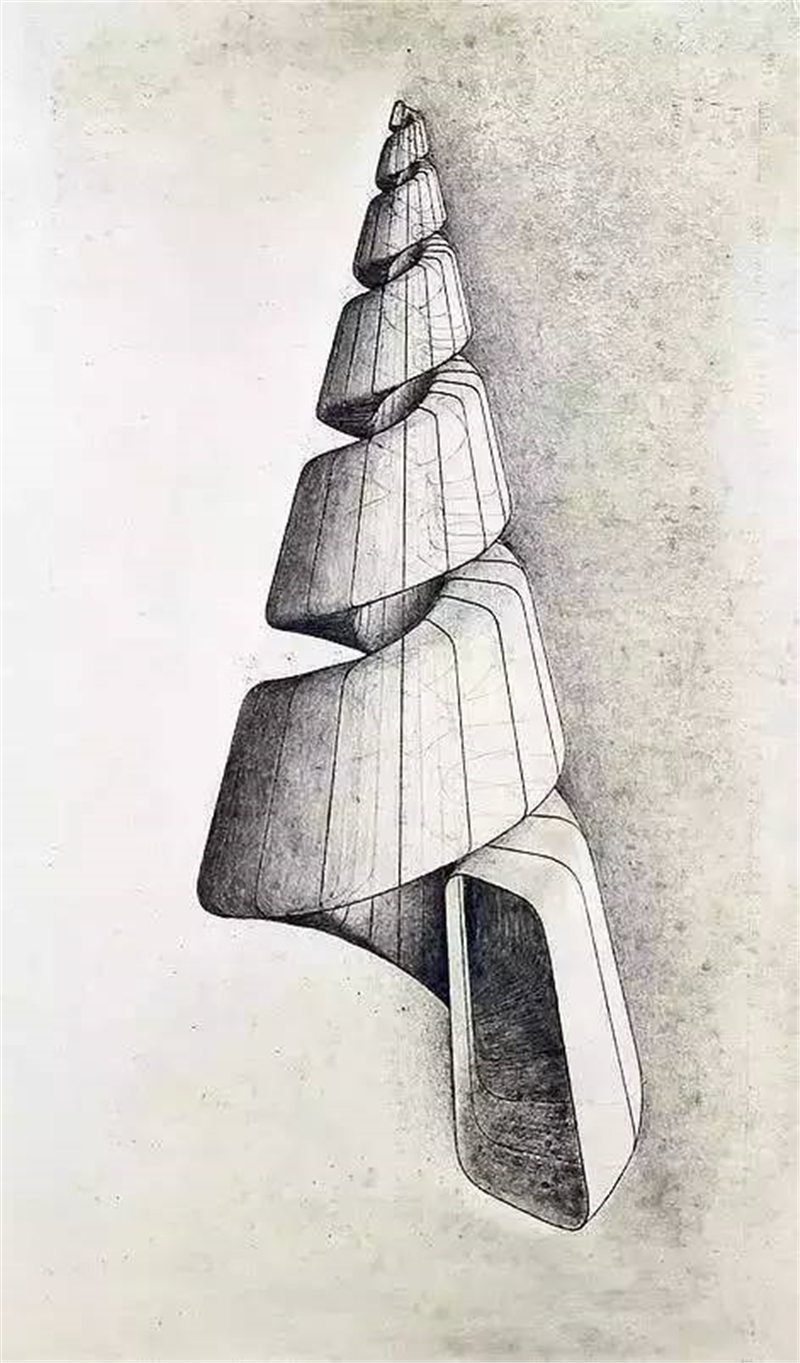
同样的还有海螺，
每当我们去海边捡贝壳、捡海螺的时候，
都会惊叹它们的外形是如此美丽。
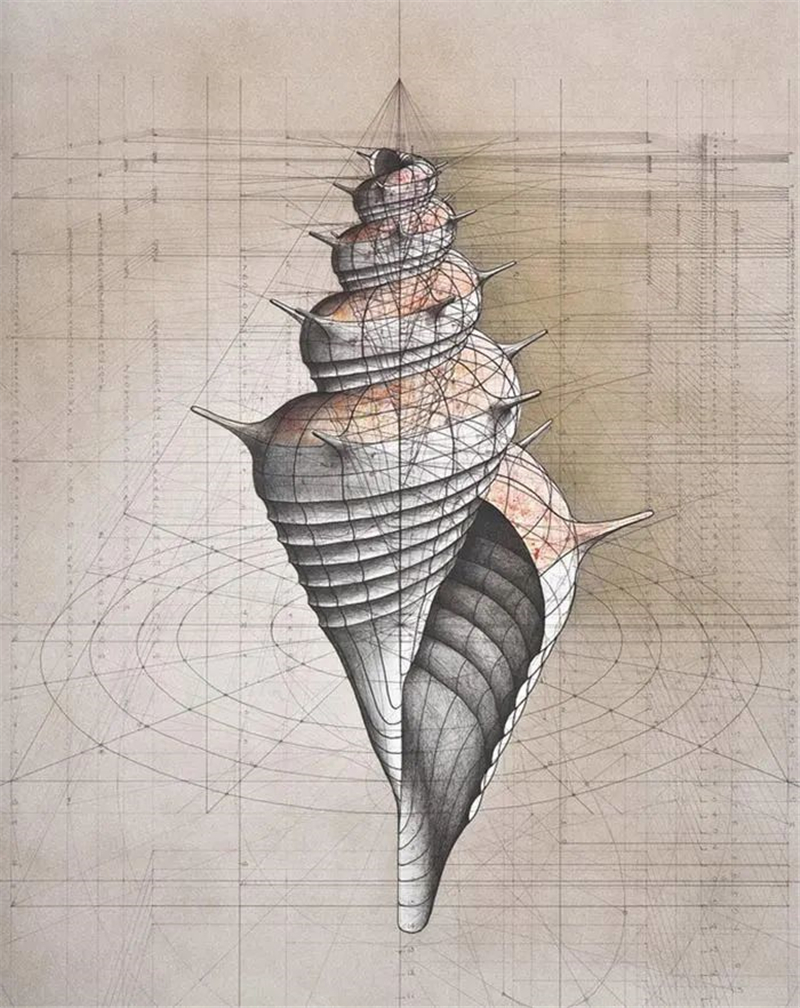
海螺生成需要遵循三个基本法则：
扩张、旋转和扭转。
所有的海螺，
都是先由一个很小很细的空心圆锥慢慢扩张、旋转、
扭转而形成的螺旋体，
该螺旋体一直是增量扩张，螺口最大。
尽管螺形状各式各样、千奇百怪，
但都是全部遵循螺旋线，
包括但不限于：
等角螺线、阿基米德螺线、费马螺线、
等角螺线、双曲螺线、圆内螺线等等
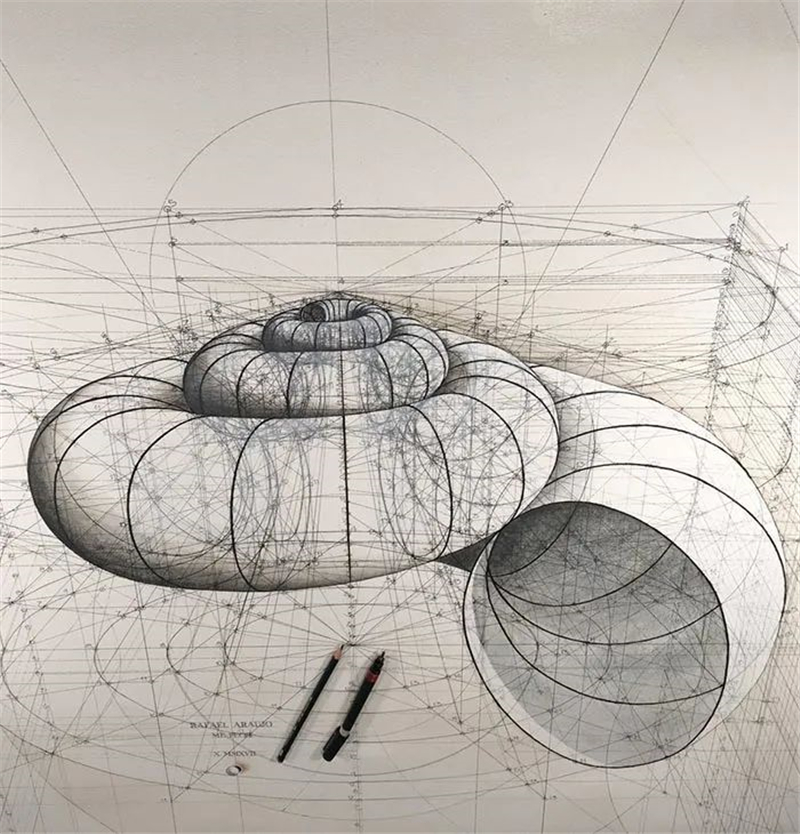
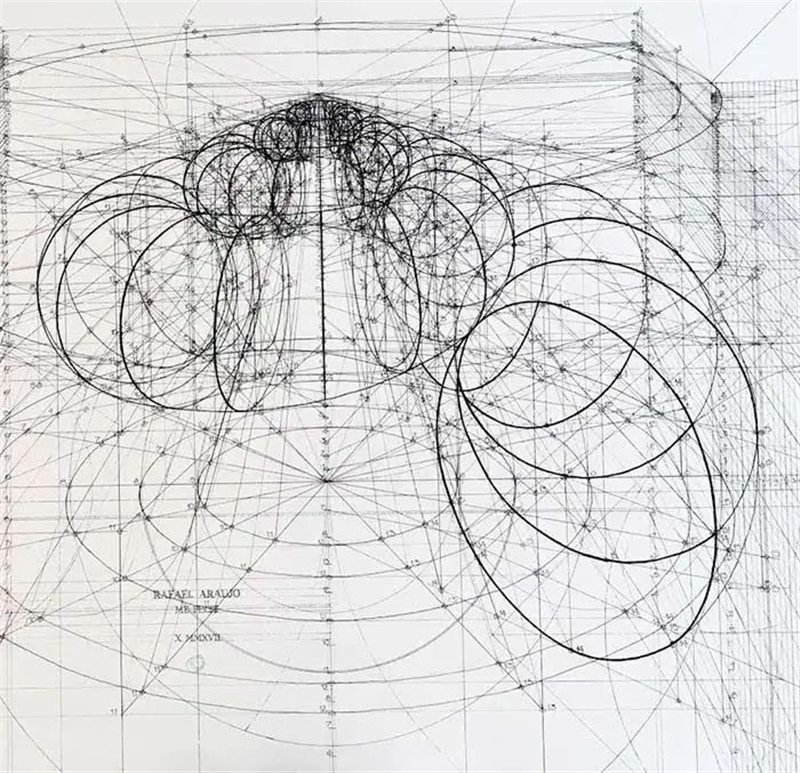
倘若你把这些螺旋线画出来，
你也能得到一个完美的海螺图形。
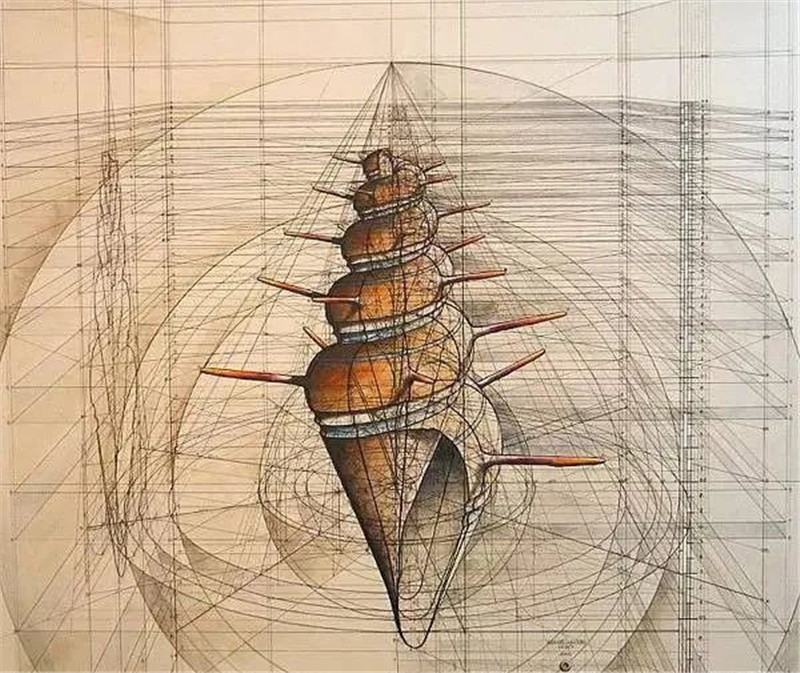
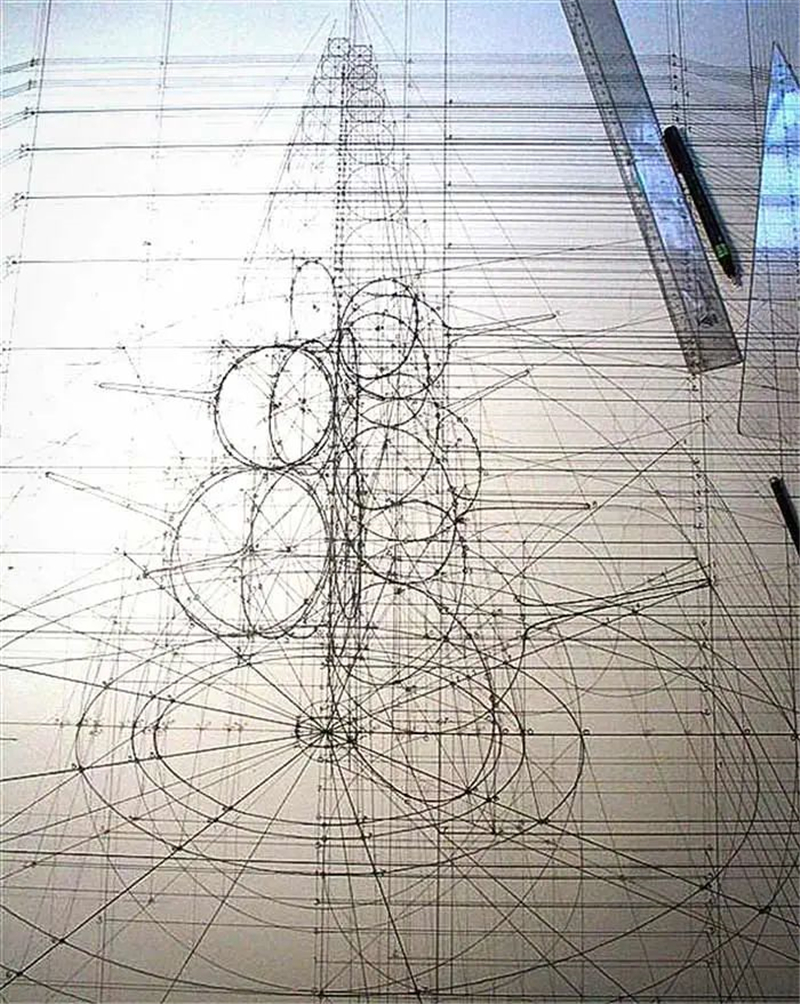
无论海螺、蝴蝶还是山茶花，
其实都是从一些基本图形上演变而来的。
这些基本图形，就是几何图形。
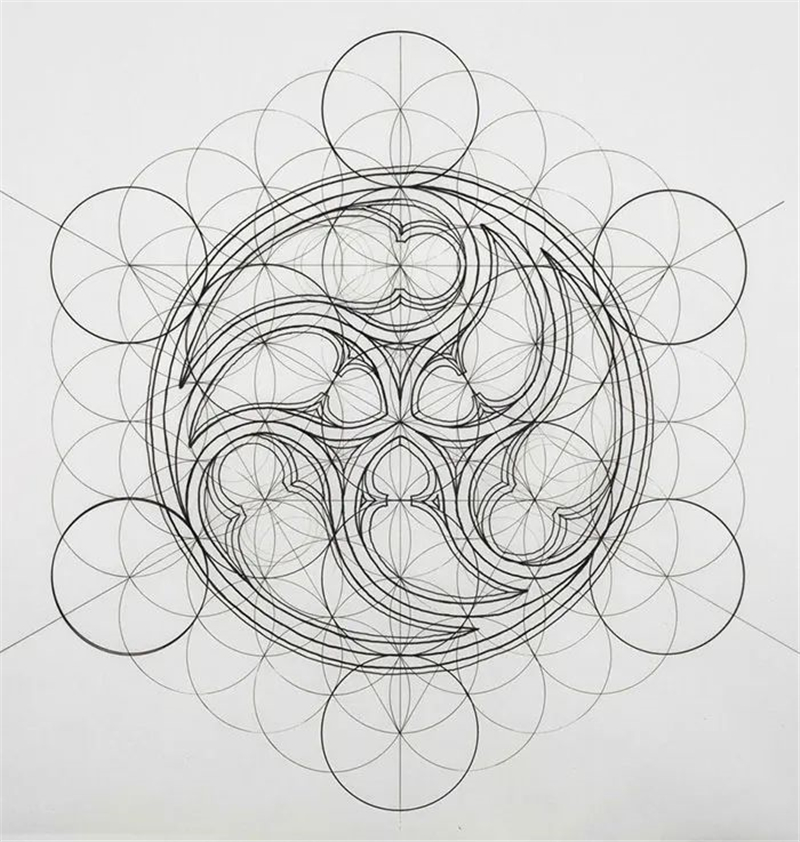
几何图形，
也符合黄金比例的规律。
我们常说的黄金三角形，
就符合1:1.618的黄金比例。
建立在黄金比例，
和其他数学理论基础上的蝴蝶，
也呈现出一种完美的飞翔姿态和轨迹，
多一寸则太多，少一寸则太少。
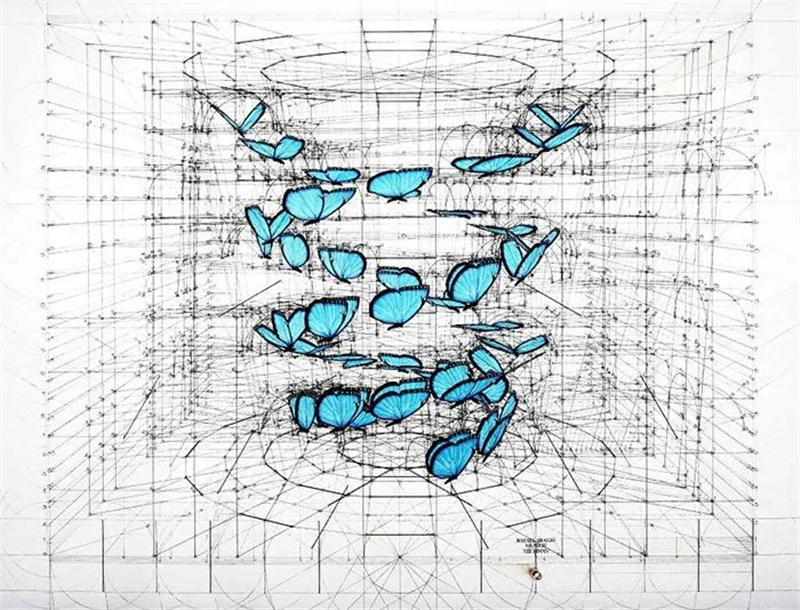
千万别小看一只蝴蝶，
背后的可视化数学框架，
说不定就是火箭的核心秘密，
毕竟蝴蝶在大洋彼岸扇动一下翅膀，
就能引来一场海啸。
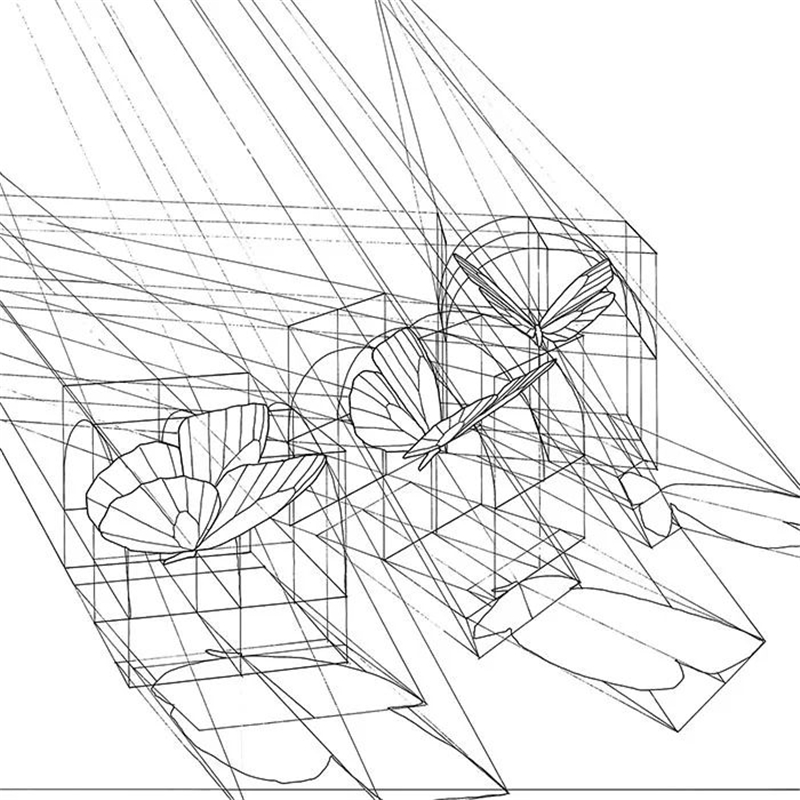
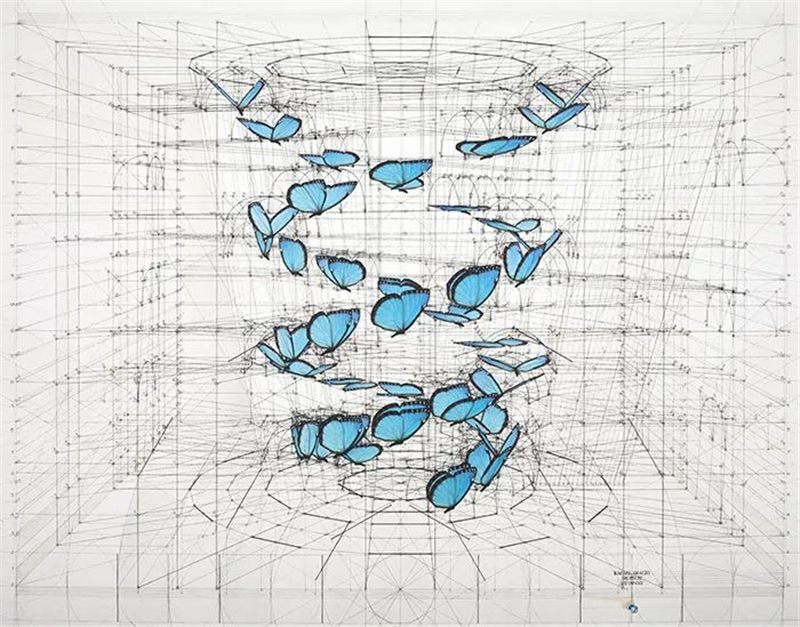
这一模型也可以用在建筑上，
让建筑呈现更稳固的结构和更精美的外观。
而且，
真正的艺术与美，
从来不是艺术馆里束之高阁的藏品，
而是自然界中的生灵与万物。
大自然才是真正的鬼斧神工：
一只飞舞的蝴蝶，就是美的极致，
美就在我们身边。
文章来源于网络，如有不妥，可联系删除
